Given two point A and B. If the initial point of coordinate system is O, then we get vector OA and vector OB. We do not use it in common. If vector OA = v, and the later is u, we know that O, A, and B form a triangle that follow the law of Cosines.
This law is below
|AB|^2 = |OA|^2 + |OB|^2 - 2. |OA|. |OB| cos x, if x is angle AOB.
We represent the equation above in vector u and v as below.
|v - u|^2 = |u|^2 + |v|^2 - 2|v||u|cos x
Remember that |v|^2 = v.v (dot product of vector v)
(v - u).(v - u) = u.u + v.v - 2.|u|.|v| cos x
v.v - 2.u.v + u.u = u.u + v.v - 2 |u||v| cos x
so cos x is equal to
cos x = u.v / |u||v|
IntroducMath
Sunday, May 29, 2011
Position on Earth
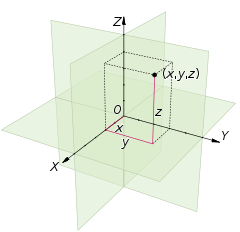
Earth, more precision, have more density on its equator. Which means, the distance to the earth's core from equator is greatest than other surface of earth. For some reason, we assumed that earth as a sphere that every P on surface have an equal distance to the core. On three dimensional space, we used Cartesian coordinate for 3D object as below.
Three dimensional Cartesian coordinate placed a point A relatively to the O, the initial point of the coordinate system. Picture placed a point called (x,y,z) on that coordinate. But on earth, we will challenge a difficulties to find the value of x, y, and z as pictures. So, we used other coordinate system that more easily to use.
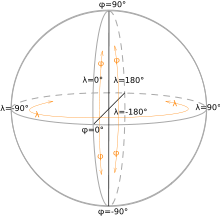
First we assume the radius of earth is equal in each P on surface that equal to R. Second, we measure an height angle from equator that called latitude (phi). Positive if its above the equator, and negative for the opposite. The Third, we measure the distance angle from the meridian line that through Greenwich in England that called longitude (lamda). So we could graph earth as below.
On a polar coordinate system, a point A on surface of earth is (r, phi, lamda). This coordinate can be transformed to Cartesian models as {r cos (phi) cos (lamda), r sin (lamda) cos (phi), r sin (phi)}.
Three dimensional Cartesian coordinate placed a point A relatively to the O, the initial point of the coordinate system. Picture placed a point called (x,y,z) on that coordinate. But on earth, we will challenge a difficulties to find the value of x, y, and z as pictures. So, we used other coordinate system that more easily to use.
First we assume the radius of earth is equal in each P on surface that equal to R. Second, we measure an height angle from equator that called latitude (phi). Positive if its above the equator, and negative for the opposite. The Third, we measure the distance angle from the meridian line that through Greenwich in England that called longitude (lamda). So we could graph earth as below.
On a polar coordinate system, a point A on surface of earth is (r, phi, lamda). This coordinate can be transformed to Cartesian models as {r cos (phi) cos (lamda), r sin (lamda) cos (phi), r sin (phi)}.
Radian in Advance, Limit ratio of an angle and its sines
One of the important limit when you learn calculus is limit of ratio of an angle and its sines. We got the value from this steps. Let we have a pie on a circle that have a central point O and the pie was sign on a arc AB. Let OA be horisontal line. From B we determine projection point on OA called C, that the area of triangle OBC always less than pie OAB. Next extend OB to point D that the projector of D on OA is A itself. That area of triangle OAD always greater than pie OAB ones.
|OC||BC|:2 < angle(AOB) . |OA|^2 : 2 < |OA||AD| : 2
Using a proportion of trigonometry, we know that |OC| = |OA| sin angle(AOB), |AD| = |OA| tan angle(AOB)
sin(angle(AOB)) < angle(AOB) < tan(angle(AOB))
We get the ratio of an angle and its sines by dividing all with sin(angle(AOB)), if the angle we symbolize with x, so we get,
1 < x/sin x < 1/cos x
We know that lim c = c, for a constant c, and limit 1/cos x equal to 1 for x toward 0. On advance of calculus, you will find that if a<b<c, lim a = lim c, so lim b = lim a = lim c. With it, we got
lim(x -> 0) x/sin x = 1
|OC||BC|:2 < angle(AOB) . |OA|^2 : 2 < |OA||AD| : 2
Using a proportion of trigonometry, we know that |OC| = |OA| sin angle(AOB), |AD| = |OA| tan angle(AOB)
sin(angle(AOB)) < angle(AOB) < tan(angle(AOB))
We get the ratio of an angle and its sines by dividing all with sin(angle(AOB)), if the angle we symbolize with x, so we get,
1 < x/sin x < 1/cos x
We know that lim c = c, for a constant c, and limit 1/cos x equal to 1 for x toward 0. On advance of calculus, you will find that if a<b<c, lim a = lim c, so lim b = lim a = lim c. With it, we got
lim(x -> 0) x/sin x = 1
Radian in Advance, Arc length
When you go to school, you know that there r two kind of measure of an angle. Degree and radian. For some reason, i like to used degree. Because its visual intuitive, and give me more 'real' story on studying angles. International standard takes radian as the standard measure of degree. Its because radian had some advance.
Radian itself define as a ratio between the length of an arc and its radius. So the main advance is arc length. Ratio between arc and circumstance of a circle is equal to ratio between the central angle and 360 degree angle.
arc(AB) : 2(phi)R = deg(x) : deg(360)
arc(AB) = 2(phi)/deg(360) . deg(x) . R
if y is representative of x on radian, then the equation become
arc(AB) = y.R
so, Given a circle with radius R, length of an arc AB on the circle equal to the multiplication of the radius R and its central angle on radian measure.
Radian itself define as a ratio between the length of an arc and its radius. So the main advance is arc length. Ratio between arc and circumstance of a circle is equal to ratio between the central angle and 360 degree angle.
arc(AB) : 2(phi)R = deg(x) : deg(360)
arc(AB) = 2(phi)/deg(360) . deg(x) . R
if y is representative of x on radian, then the equation become
arc(AB) = y.R
so, Given a circle with radius R, length of an arc AB on the circle equal to the multiplication of the radius R and its central angle on radian measure.
Saturday, May 28, 2011
My Geometry, object of intuitive world
Sometimes i do not learn math for the skill or for educate even not for a mathematics things. I just step my foot right to the class. I don't get what it mean, i don't get what it about, but i feel some sense of happy and its just pass me by.
This is when my first class of Geometry. I build my intuitive even its wrong, n i do not care bout that. First, Euclidesan geometric. I love to think it like a mapping our own style of thinking. I do not find an euclidean object on any room, but it's in my mind. When i walk in to my mind, i don't even know where to start or where its should end. Its like a swimming on God will. As euclidean want, if i put an 8, so add one on that and i got 9. I can put any one on any numbers i like. I don't know where to start n where to end. Even when you tell me a cube and it will be figured in my mind right cube. Right mean its real cube with the properties they should be. So intuitively i say that euclidean was on my mind.
When i start to belief on Euclidean, i figure out that its not real at all, since my first time heard bout Lobachevsky's works. I realize that in my visual space, everything is curved. I saw a cubical object, but it curved. I walk in an highway but its curved. When something move outward us, their spatial properties decrease in curve. As when we walk to some object, they will increase its spatial properties. Its real and the things is exist as Lobachevsky say.
I feel i'm on the end of journey, but its not true. I realize that in our perfect world, euclidean, we could predict and models what happen to the 'real'. When i think its complete on Euclid and Lobachevsky, Riemann bring other new world. As like I heard someone says, 'when you become clever enough, your limit is no more than an illusion." Yes, i think if i draw a line on a planar object, they will length in space for unlimited being. But I realize that it may exist other room, other space, other geometric being that if i drew a line, i will meet its tail exactly on the starting point. Yup, I imagine how earth can be the real models of what Riemann brings. Its like we walk to outer space, watch and learn about where we are in exist.
Its crazy even i haven't learn it all yet. Its just my imagination say that time over time. Now when i realize it, i think maybe we could say that the space, is not just an image. It will be more easy if we describe it on an object-properties-method view, or on an analysis based on Tensor. I don't know where will i stop to realize, but its a nice trip n fantasy. May be you can teach me well on what really they are, right before my imagination goes wild.
This is when my first class of Geometry. I build my intuitive even its wrong, n i do not care bout that. First, Euclidesan geometric. I love to think it like a mapping our own style of thinking. I do not find an euclidean object on any room, but it's in my mind. When i walk in to my mind, i don't even know where to start or where its should end. Its like a swimming on God will. As euclidean want, if i put an 8, so add one on that and i got 9. I can put any one on any numbers i like. I don't know where to start n where to end. Even when you tell me a cube and it will be figured in my mind right cube. Right mean its real cube with the properties they should be. So intuitively i say that euclidean was on my mind.
When i start to belief on Euclidean, i figure out that its not real at all, since my first time heard bout Lobachevsky's works. I realize that in my visual space, everything is curved. I saw a cubical object, but it curved. I walk in an highway but its curved. When something move outward us, their spatial properties decrease in curve. As when we walk to some object, they will increase its spatial properties. Its real and the things is exist as Lobachevsky say.
I feel i'm on the end of journey, but its not true. I realize that in our perfect world, euclidean, we could predict and models what happen to the 'real'. When i think its complete on Euclid and Lobachevsky, Riemann bring other new world. As like I heard someone says, 'when you become clever enough, your limit is no more than an illusion." Yes, i think if i draw a line on a planar object, they will length in space for unlimited being. But I realize that it may exist other room, other space, other geometric being that if i drew a line, i will meet its tail exactly on the starting point. Yup, I imagine how earth can be the real models of what Riemann brings. Its like we walk to outer space, watch and learn about where we are in exist.
Its crazy even i haven't learn it all yet. Its just my imagination say that time over time. Now when i realize it, i think maybe we could say that the space, is not just an image. It will be more easy if we describe it on an object-properties-method view, or on an analysis based on Tensor. I don't know where will i stop to realize, but its a nice trip n fantasy. May be you can teach me well on what really they are, right before my imagination goes wild.
Saturday, May 14, 2011
Introduction on Structure, or its an abstract algebra
Sometimes we asked ourself, math? what for? and Some question unanswered. This is my first time learning abstract algebra. only What for remain in my head and its does lead for nothing. Unlike other mathematics branch, we found the useful of math in no time. Say trigonometri, algebra, calculus. But when i got structure class.. blind at all.
Ok, then my advisor tell me. Imagine that you have to be first time human on earth that sent to study outside our solar systems. You met extra terrestrial being. You have to learn their knowledge as an ambassador of mankind. Then you walk into class. You met a new, over new, faces. Even you can't say it faces. Then you start to learn.
Then you heard the teacher say, 'gorifsd'. And all of student answer, 'yuke'. You may not know how exactly what they say, but you could feel or sense that maybe its like our greetings. Then they continue with the class. Teacher say, 'ouri pur koe', while student say, 'tudi'. Next teacher say, 'ouri pur firk', student answer with, 'ikre'. Yeah, you may guess anything, but how bout addition?
Imagine that in that society, 'pur' is a kind of operation. Then 'ouri, koe, firk, tudi, ikre,' is somewhat as number than relate each other especially by operation 'pur'. Yeah, it can be anything. But thinking like that helpful for some degree i though. Then we can general our knowledge of operation and sets. We think that 1 + 2 always equal to 3. But, if we define '+' and '=' on other way, so far that we could not predict what happen to our number, what is rules, or other building of knowledge that keep it consistent?
When you studying structure, we will find a new world and new point of view. When it make sense, we will know that our knowledge is a gift for living. Also we could be wise. The other, its build math consistent and applicable on any given condition, even it doesn't mean math could satisfy any condition. For starting, you should try to read "Alice adventure in wonderland". Its a good movie and full of logical term.
Ok, then my advisor tell me. Imagine that you have to be first time human on earth that sent to study outside our solar systems. You met extra terrestrial being. You have to learn their knowledge as an ambassador of mankind. Then you walk into class. You met a new, over new, faces. Even you can't say it faces. Then you start to learn.
Then you heard the teacher say, 'gorifsd'. And all of student answer, 'yuke'. You may not know how exactly what they say, but you could feel or sense that maybe its like our greetings. Then they continue with the class. Teacher say, 'ouri pur koe', while student say, 'tudi'. Next teacher say, 'ouri pur firk', student answer with, 'ikre'. Yeah, you may guess anything, but how bout addition?
Imagine that in that society, 'pur' is a kind of operation. Then 'ouri, koe, firk, tudi, ikre,' is somewhat as number than relate each other especially by operation 'pur'. Yeah, it can be anything. But thinking like that helpful for some degree i though. Then we can general our knowledge of operation and sets. We think that 1 + 2 always equal to 3. But, if we define '+' and '=' on other way, so far that we could not predict what happen to our number, what is rules, or other building of knowledge that keep it consistent?
When you studying structure, we will find a new world and new point of view. When it make sense, we will know that our knowledge is a gift for living. Also we could be wise. The other, its build math consistent and applicable on any given condition, even it doesn't mean math could satisfy any condition. For starting, you should try to read "Alice adventure in wonderland". Its a good movie and full of logical term.
Monday, May 9, 2011
How Right Triangle become important part of Trigonometry
Trigonometry, means the measure on a trigonal. Formally we say that trigonometry is branch in mathematics that studies triangle and the relation between the angles and the sides. When you learn it at school, you know that right triangle become an important part. Why? and where it come from?
Let we talk bout the property of congruent triangle. They say that if two triangle is congruent, which mean the associate angle is equal, proportion of its associate sides is equal to each other.
Lets use it in trigonometry. Trigonometry relate an angle of a triangle to the proportion of it sides. Since we use an angle, not angles, we do not have any suggestion where triangle in question. Say 30 degree of an angle, so we can build up unlimited triangle of it.
Thats the key to trigonometry of right triangle. On a right triangle, if we define a degree (of course which absolute of it should less then 90 and not equal to zero), we can build an unlimited triangle, but with special property that they are congruent. Since the congruency tell us that its not affect on the angles and the proportion of sides (note its not their weight or length), so on a right triangle, an angle is relate to proportion of two sides. if the sides describe depend on the unique angle, we can listed trigonometric proportion of right triangle below.
sin a = opposite/hypotenuse
cos a = adjacent/hypotenuse
tan a = opposite/adjacent
hypotenuse is familiar term on right triangle specially when you talking pythagorean. Opposite and adjacent is side that depend on the unique angle 'a'. And the sin, cos, tan, is refer to sines, cosines, and tangent as a trigonometric function.
That is a unique of an angle on right triangle, that combine with the congruency of triangle, build up a trigonometric proportion. in extend of that proportion, there are several function that related to the mention above is secant, cosecant, and cotangent. This is how math build on your mind.
Let we talk bout the property of congruent triangle. They say that if two triangle is congruent, which mean the associate angle is equal, proportion of its associate sides is equal to each other.
Lets use it in trigonometry. Trigonometry relate an angle of a triangle to the proportion of it sides. Since we use an angle, not angles, we do not have any suggestion where triangle in question. Say 30 degree of an angle, so we can build up unlimited triangle of it.
Thats the key to trigonometry of right triangle. On a right triangle, if we define a degree (of course which absolute of it should less then 90 and not equal to zero), we can build an unlimited triangle, but with special property that they are congruent. Since the congruency tell us that its not affect on the angles and the proportion of sides (note its not their weight or length), so on a right triangle, an angle is relate to proportion of two sides. if the sides describe depend on the unique angle, we can listed trigonometric proportion of right triangle below.
sin a = opposite/hypotenuse
cos a = adjacent/hypotenuse
tan a = opposite/adjacent
hypotenuse is familiar term on right triangle specially when you talking pythagorean. Opposite and adjacent is side that depend on the unique angle 'a'. And the sin, cos, tan, is refer to sines, cosines, and tangent as a trigonometric function.
That is a unique of an angle on right triangle, that combine with the congruency of triangle, build up a trigonometric proportion. in extend of that proportion, there are several function that related to the mention above is secant, cosecant, and cotangent. This is how math build on your mind.
Subscribe to:
Comments (Atom)